2122A. Greedy Grid

题意

定义 Greedy Path 为：从左上角出发，每次向右或下的相邻一格移动，且移动的格子的值不小于另一个选择。

路径的值为：经过的所有格子权值之和。

问题：存不存在 $n \times m$ 的由非负整数组成的网格，满足没有 Greedy Path 的值达到“所有向(右/下)走的路径的值的最大值”？

解法

思路

Greedy Path 会向大的方向走，因此考虑一种设计网格的方案：把 Greedy Path “引诱” 到一条起始格非常大、后面都很小的路径上；再构造一条起始小、后面非常大的路径，使这条路径值大于 Greedy Path 即可。

图为 $3 \times 3$ 的例子：

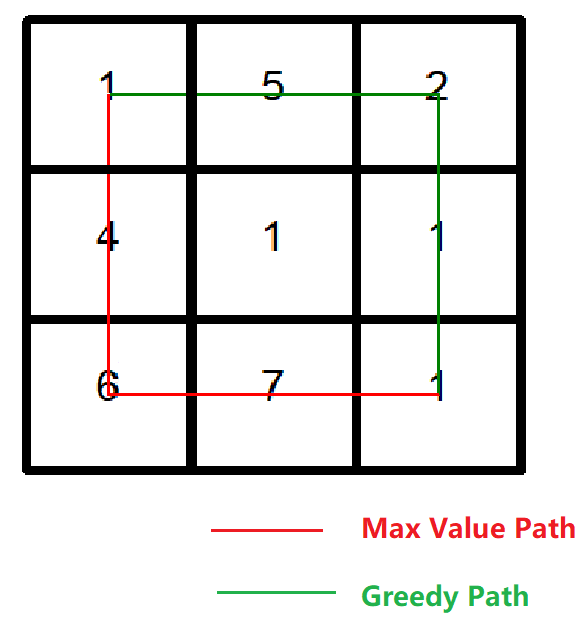
什么时候无法构造出这样的网格呢？

1. 只有一条路径，即 $n = 1$ 或 $m = 1$；
2. 两条路径不重合的部分只有一个点，即 $n = m = 2$。（假设构造的是 $a_{1, 2} > a_{2, 1}$，由于 $a_{1, 1} + a_{1, 2} + a_{2, 2} > a_{1, 1} + a_{2, 1} + a_{2, 2}$，两种路径会重合）

结论

$n = 1$ 或 $m = 1$ 时，只有一条路径，因此输出 No；

$n = m = 2$ 时，只有两条路径，因为 Greedy Path 会走向值较大的格，最大值的路线也是这样，所以 Greedy Path 的路线和最大值路线一定是一样的，也输出 No。

容易证明，其他情况下都存在满足题意的网格，输出 Yes。

参考代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

#include <iostream>

using namespace std;

int main() {
	int t;
	cin >> t;
	while (t -- ) {
		int n, m;
		cin >> n >> m;
		if (n == 1 || m == 1 || (n == 2 && m == 2)) puts("No");
		else puts("Yes");
	}
	return 0;
}

2122B. Pile Shuffling

题意

你有 $n$ 摞数字，每摞由 $a_i$ 个 0 和 $b_i$ 个 1 组成，其中 0 在上面，1 在下面。

每次操作你只能将任意一摞数字的最上方的一个数移动到任意一摞的任意位置。

最终要求每一摞数字由上面的 $c_i$ 个 0 和下面的 $d_i$ 个 1 组成，输出最小操作次数。

解法

思路

只考虑挪出数字的情况。

• 若 $b_i > d_i$，我们需要将所有上面的 0 挪开（到本摞要挪走的最靠下一个 1 的下面或到其他堆），操作次数是 $\min(a_i, c_i) + b_i - d_i$（因为可以先挪 1，也可以后挪 1）。
• 若 $a_i > c_i$，我们需要将 $a_i - c_i$ 个 0 挪走，操作次数是 $a_i - c_i$。

结论

对于每堆数字：

• 若 $a_i > c_i$，$ans += a_i - c_i$。

• 若 $b_i > d_i$，$ans += a_i + b_i - d_i$。

参考代码

赛时没关同步过了，刚刚交的不关同步过不了？

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include <iostream>

using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);

	int t;
	cin >> t;
	while (t -- ) {
		int n;
		cin >> n;

		long long ans = 0;
		while (n -- ) {
			int a, b, c, d;
			cin >> a >> b >> c >> d;
			if (a > c) ans += a - c;
			if (b > d) ans += min(a, c) + b - d;
		}
		cout << ans << endl;
	}
	return 0;
}

2122C. Manhattan Pairs

题意

将 $n$ 个点分成 $\frac{n}{2}$ 对，使得每对点之间的曼哈顿距离之和最大。输出任意一种配对方案。

保证 $\sum{n} \leq 2 \times 10^5$，$n$ 是偶数。

解法

思路

考虑一维情况，最优方案是将最小的 $\frac{n}{2}$ 个点与最大的 $\frac{n}{2}$ 个点配对。

那么开始考虑二维情况，最优方案显然是：

• $x$ 坐标最小的 $\frac{n}{2}$ 个点（定义为 $X_l$）与最大的 $\frac{n}{2}$ 个点（定义为 $X_r$）配对；
• $y$ 坐标最小的 $\frac{n}{2}$ 个点（定义为 $Y_l$）与最大的 $\frac{n}{2}$ 个点（定义为 $Y_r$）配对。

所以我们将所有点分成 $4$ 部分处理：

• $X_l \cap Y_l$ 与 $X_r \cap Y_r$ 配对；
• $X_l \cap Y_r$ 与 $Y_r \cap Y_l$ 配对。

设：

• $|X_l \cap Y_l| = a$
• $|X_r \cap Y_r| = b$
• $|X_l \cap Y_r| = c$
• $|Y_r \cap Y_l| = d$

那么有：

• $a + c = b + d$，因为 $|X_l| = |X_r|$；
• $a + d = b + c$，因为 $|Y_l| = |Y_r|$。

两式相加、移项、系数化为1 后可得：$a = b$ 和 $c = d$，所以刚刚提到的配对方法不会出现剩下的点。

结论

• $X_l \cap Y_l$ 与 $X_r \cap Y_r$ 配对；
• $X_l \cap Y_r$ 与 $X_r \cap Y_l$ 配对。

参考代码

参考了 Tourist 的解法，通过三次排序分出了四组。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 2e5 + 10;

int x[N], y[N], idx[N];

int main() {
	int t;
	cin >> t;
	while (t -- ) {
		int n;
		cin >> n;
		for (int i = 0; i < n; i ++ ) {
			cin >> x[i] >> y[i];
			idx[i] = i;
		}
		sort(idx, idx + n, [&](int i, int j) {return x[i] < x[j];});
		sort(idx, idx + n / 2, [&](int i, int j) {return y[i] < y[j];});
		sort(idx + n / 2, idx + n, [&](int i, int j) {return y[i] < y[j];});
		// Xl&Yl, Xl&Yr, Xr&Yl, Xr&Yr
		for (int i = 0; i < n / 2; i ++ ) {
			cout << idx[i] + 1 << ' ' << idx[n - 1 - i] + 1 << endl;
		}
	}
	return 0;
}